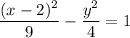I need help look at the image attached

Question

asked Jun 24, 2023 129k views

1 Answer

Grey Perez · Answer 1 · 2023-06-29T11:57:28+0000

Answer:

((x-2)^2)/(9)-(y^2)/(4)=1

Explanation:

Given points:

Standard equation of a horizontal hyperbola (opening left and right):

$\boxed{((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1}$

where:

Points (5, 0) and (-1, 0) are the vertices of the hyperbola.

The center (h, k) is midway between the vertices. Therefore:

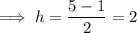
$\implies h=(5-1)/(2)=2$

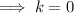
$\implies k=0$

Substitute the found values of h and k into the formula:

((x-2)^2)/(a^2)-(y^2)/(b^2)=1

Substitute point (5, 0) and solve for a²:

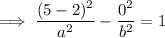
$\implies ((5-2)^2)/(a^2)-(0^2)/(b^2)=1$

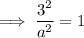
$\implies (3^2)/(a^2)=1$

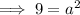
$\implies (9)/(a^2)=1$

$\implies 9=a^2$

Substitute one of the (2±3√2, ±2) points and the found value of a² and solve for b²:

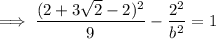
$\implies ((2+3√(2)-2)^2)/(9)-(2^2)/(b^2)=1$

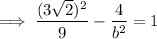
$\implies ((3√(2))^2)/(9)-(4)/(b^2)=1$

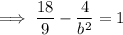
$\implies (18)/(9)-(4)/(b^2)=1$

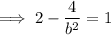
$\implies 2-(4)/(b^2)=1$

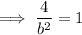
$\implies (4)/(b^2)=1$

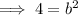
$\implies 4=b^2$

Substitute the found values of a² and b², together with the values of h and k, into the formula to create the equation of the hyperbola:

((x-2)^2)/(9)-(y^2)/(4)=1