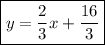Question

The support arm, AB, is

perpendicular to a line tangent to this curve on a roller coaster at the point of tangency B.

The equation of the tangent line to the curve at B is 3x + 2y = 28.

Find the equation of the support arm, AB.
B(4,8)

Lines perpendicular to tangents to curves, at
the point of tangency, are referred to as “normals.”

Answer 1

`y = (2)/(3)x + (16)/(3)}`

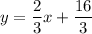
Explanation:

The genera slope-intercept equation of a line is

y = mx + 8 where m is the slope and b the y-interecept

A perpendicular line will have a slope = -1/m ie the negative of reciprocal of the first line such that m x (-1/m ) = -1

The equation of the tangent line is

3x + 2y = 28.

1. Convert to slope-intercept form:

• Subtract 3x from both sides
  3x - 3x + 2y = 28 - 3x
  2y = 28 - 3x
  y = 14 - 3/2x
• y = (-3/2)x + 14

So slope = -3/2

Reciprocal of -3/2 = -2/3
Negative of reciprocal = +2/3

Slope of a perpendicular line should be -1/3 and the resultant equation of the line(the support arm) should be:

y = (2/3)x + b

To calculate b for the complete line equation plug in the point B(4, 8) and solve for B

y = 8 when x = 4

=> 8 = (2/3)(4) + b

Switch sides: (does not change any signs)
8/3 + b = 8

Subtract 8/3 on both sides
b = 8 - 8/3

b = 24/3 - 8/3

b = 16/3

So equation of the support arm is

`\boxed{y = (2)/(3)x + (16)/(3)}`