Question

A car travels a distance of 100km for 1h38min45sec.a)Round off the time to the nearest 1/4 hour b)Use the rounded time to find the average speed for the journey​

Answer 1

Answer: 57.14 km/hr

Step-by-step explanation: if an hour is divided into quarters it will be in increments of 15 minutes, since one hour is 60 minutes. 60 minutes divided by 5 is 15 minutes.

So 1 hour and 38 minutes is rounded off to 1 hour and 45 minutes.

this is 1 hour + 3/4 hour = 1 3/4 hour. This is same as 1.75 hour

3/4 is .75

speed divided by the time will give the average speed.

100km/1.75hours = 57.14 km/per hour

Answer 2

(a) 1 hour 45 min

(b) 57.1 km/h (nearest tenth)

Explanation:

Given information:

• Distance = 100 km
• Time = 1 h 38 min 45 sec

`\large\boxed{\sf Speed=(Distance)/(Time)}`

Part (a)

`\begin{aligned}\sf (1)/(4)\;hour &= \sf 1 \; hour / 4 \\& = \sf 60 \;mins / 4\\& = \sf 15 \; mins\end{aligned}`

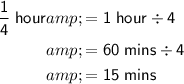
Therefore, the nearest ¹/₄ hours either side of the given time is:

• 1 hour 30 min
• 1 hour 45 min

1 h 38 min 45 sec is 8 min 45 sec more than 1 hour 30 min.

1 h 38 min 45 sec is 6 min 15 sec less than 1 hour 45 min.

Therefore, the nearest ¹/₄ hour to the given time is:

• 1 hour 45 min.

Part (b)

1 hour 45 min = 1.75 min (in decimal form)

Substitute the given distance and the rounded time (in decimal form) into the formula and solve for speed:

`\begin{aligned} \implies \sf Speed & =\sf (Distance)/(Time)\\\\& = \sf (100)/(1.75)\\\\& = \sf 57.1\;km/h\;(nearest\;tenth)\end{aligned}`