Question

Use the quadratic formula to solve: 3x² + 4x + 2 = 0.

What is the value of the discriminant?
What does this tell you about the solutions to the equation?

Answer 1

`x=-(2)/(3)+(√(2))/(3)i\\\\x=-(2)/(3)-(√(2))/(3)i`

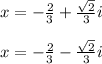
Explanation:

The Quadratic Formula gives us the roots of a quadratic and is defined as:
`x=(-b\pm√(b^2-4ac))/(2a)`

The discriminant is the part in the square root which is:
`b^2-4ac`

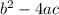
if the discriminant of the quadratic is zero, then the quadratic only has one distinct zero with a multiplicity of 2.

To see why, let's plug in zero for the discriminant:
`x=(-b\pm√(0))/(2a)`

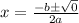
The square root of zero is just going to be zero:
`x=(-b\pm0)/(2a)`

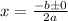
Adding or subtracting zero doesn't change the value:
`x=(-b)/(2a)`

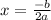
As you can see here it doesn't matter if we take the positive or negative solution, we'll get one value.

If the discriminant of the quadratic is positive, then the quadratic will have two distinct real solutions.

Well the solutions are real because the square root has real solutions for positive numbers. The reason we have two distinct solutions is because the square root of a positive number will have a positive and negative solution. These square roots will have a non-zero value and will affect the value of the numerator based on whether you take the negative or positive solution giving you two distinct solutions.

If the discriminant of the quadratic is negative, then the quadratic will have two distinct complex solutions.

To clarify, real numbers are technically complex numbers, since complex numbers are just:
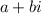`a+bi`, where a=real part, and b=imaginary part. We could use this to represent any real number where b=0.

So when I'm saying "complex solution" I mean a complex solution where b does not equal zero, so there is a non-zero imaginary component to the complex solution.

The reason we have a complex solution in the first place is because we have a negative number in the square root. The square root only has real solutions for positive numbers, since any real number squared will give you a positive number regardless of the sign (positive or negative). The only number that is negative when squared is an imaginary number.

The reason we have two distinct solutions is actually the same reason we have two distinct solutions when the discriminant is positive. Since the square root will yield a non-zero number, so when we add it or subtract it to b, we will get to different values for the numerator, giving us two different values, or two different solutions.

So now let's solve the equation:
`3x^2+4x+2=0`

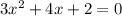
We have it in standard form where:
`ax^2+bx+c=0`

we want to use the Quadratic Formula:
`x=(-b\pm√(b^2-4ac))/(2a)`

Plugging in values we get:

`a=3,\ b=4,\ c=2\\\\x=(-4\pm√(4^2-4(3)(2)))/(2(3))\\\\x=(-4\pm√(16-24))/(6)\\\\x=(-4\pm√(-8))/(6)`

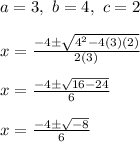
From here you'll notice the discriminant is -8, and thus we complex solutions since it's negative. We can first break up this square root into multiple square roots using the fact that:
`√(ab)=√(a)*√(b)`

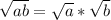
and since -8 can be defined as: -1 * 8, we can split it up like this

`x=(-4\pm√(-1)*√(8))/(6)\\\\x=(-4\pm i√(8))/(6)`

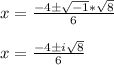
We can actually simplify the square root a bit more, since we can once more use the identity:
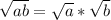`√(ab)=√(a)*√(b)`, to simplify the radical. The number 8 can be represented as 4 * 2, and sqrt(4) can be simplified easily.

`x=(-4\pm i *√(4)*√(2))/(6)\\\\x=(-4\pm 2i√(2))/(6)\\\\x=((-2 * 2)\pm2i√(2))/((3*2))\\\\x=(-2\pm i√(2))/(3)`

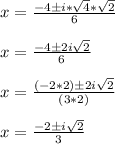
Now let's take the positive and negative solution to get the two distinct complex solutions. You can start with either but I'll just do the positive first.

Positive Solution:

`x=(-2+ i√(2))/(3)`

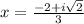
You could leave it like this, but generally whenever we have a complex number we want it in the form:
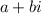`a+bi` where the real and imaginary part are separate, so we can just distribute the division of 3

Positive Solution Continued:

`x=(-2+ i√(2))/(3)\\\\x=(-2)/(3)+(√(2))/(3)i`

I also moved the "i" outside the fraction, so it's a bit easier to see the value of "b"

Negative Solution:

`x=(-2-i√(2))/(3)\\\\x=(-2)/(3)-(√(2))/(3)i`