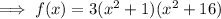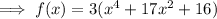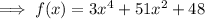Question

Find an nth-degree polynomial function with real coefficients satisfying the given conditions. If you are using a graphing utility, use it to graph the function and verify the real zeros and the given function value. N=4; i and 4i are zeros; f(-1)=102

Answer 1

`f(x)=3x^4+51x^2+48`

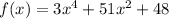
Explanation:

As n = 4, the degree of the polynomial is 4.

Therefore, the function cannot have more than 4 distinct roots.

`\implies f(x)=a(x-p)(x-q)(x-r)(x-s)`

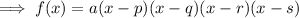
If a complex number z is a root of f(z) = 0 then its complex conjugate is also a root. Therefore:

• If i is a root, then -i is also root.
• If 4i is a root, then -4i is also root.

`\implies f(x)=a(x-i)(x+i)(x-4i)(x+4i)`

`\implies f(x)=a(x^2-i^2)(x^2-16i^2)`

`\implies f(x)=a(x^2-(-1))(x^2-16(-1))`

`\implies f(x)=a(x^2+1)(x^2+16)`

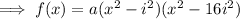
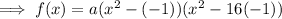
Given f(-1) = 102, then:

`\begin{aligned}\implies f(-1)=a((-1)^2+1)((-1)^2+16)&=102\\a(1+1)(1+16)&=102\\a(2)(17)&=102\\34a&=102\\a&=3\end{aligned}`

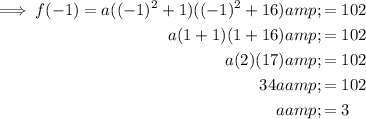
Therefore:

`\implies f(x)=3(x^2+1)(x^2+16)`

`\implies f(x)=3(x^4+17x^2+16)`

`\implies f(x)=3x^4+51x^2+48`