Answer:
A
Explanation:
using the sine ratio and the exact values
sin30° =
 and sin60° =
and sin60° =
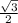
calculate the height of the wall below x , call it h
the hypotenuse is the length of the ladder
using the sine ratio in the lower right triangle.
sin30° =
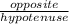 =
=
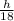 =
=
 ( cross- multiply )
( cross- multiply )
2h = 18 ( divide both sides by 2 )
h = 9
lower part of the wall is 9 meters
using the sine ratio in the right triangle on the right
sin60° =
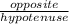 =
=
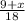 =
=
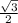 ( cross- multiply )
( cross- multiply )
2(9 + x) = 18
 ( divide both sides by 2 )
( divide both sides by 2 )
9 + x = 9
 ( subtract 9 from both sides )
( subtract 9 from both sides )
x = 9
 - 9 = 9(
- 9 = 9(
 - 1)
- 1)