Question

PLEASE HELP PHYSICS

A miniature quadcopter is located at

xi = −2.25 m

and

yi = −4.70 m

at

t = 0

and moves with an average velocity having components

vav, x = 1.70 m/s

and

vav, y = −1.50 m/s.

What are the x-coordinate and y-coordinate (in m) of the quadcopter's position at

t = 2.60 s?

Answer 1

Final coordinates in meters : (2.17, -8.6)

Step-by-step explanation:

We have the equation

displacement Δd = average velocity x time

In this case there are two components of displacement corresponding to the two components of average velocity

`v_(avg)(x) = 1.70 \; m/s`

`v_(avg)(y) = -1.50 \; m/s`

Time traveled is t = 2.60s

So the x component is toward east (+x) axis and y component is due south(-y axis)

`\sf{x \;displacement \;} \Delta_x = v_(avg)(x) x t= 1.70m/s \; * \; 2.60 = 4.42 m\\\\`

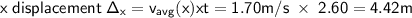
Since the original x-coordinate was at -2.25m, the end x coordinate is

x = -2.25 + 4.2 = 2.17

The y-displacement

`\sf{y \;displacement \;} \Delta_y = v_(avg)(y) x t\\\\ = - 1.50m/s \; * \; 2.60 = - 3.9 m\\\\\\\\`

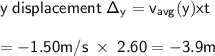
The starting y-coordinate was at y = -4.70m

So final y-coordinate = -4.7 - 3.9 = -8.6m

Final coordinates in meters : (2.17, -8.6)