Question

There are only green pens and blue pens in a box.

There are three more blue pens than green pens in the box.
There are more than 12 pens in the box.
Simon is going to take at random two pens from the box.

The probability that Simon will take two pens of the same colour is
27/55
Work out the number of green pens in the box.

Answer 1

Green Pens : 21

Explanation:

Let the number of
green pens = x

Three more blue pens than green pens translates to
=> number of blue pens = number of green pens + 3
=> blue pens = x + 3

Total number of pens = blues + green = x + 3 + x = 2x + 3

Probability of taking 2 green pens:
The first time a green pen is taken out, the probability
P( 1s green pen) = Number of green pens/Total number of pens

=
`(x)/(2x + 3)`

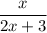
After the first green pen is removed, the number of green pens will be one less and so will the total number of pens

Number of green pens = x - 1
Total number of pens = 2x + 3 - 1 = 2x + 2

P(second green pen | first green pen)

`=(x-1)/(2x + 2)`

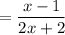
P(2 green pens) = P(first green pen) x P(second green pen)

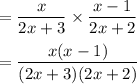`= (x)/(2x + 3) * (x-1)/(2x + 2)\\\\=(x(x -1))/((2x +3)(2x+2))` [1]

Probability of 2 blue pens

P( 1st blue pen) = number of blue pens/total number of pens

`=(x + 3)/(2x + 3)`

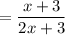
P(second blue pen = (number of pens remaining if first was blue) ÷ total number of pens - 1

If the first pen taken was blue then there will be 2x + 3 - 1 blue pens out of a total of 2x + 3 - 1 pens

P(2nd blue pen | first blue pen)

`=(x + 2)/(2x + 2)`

`\text{P(2 blue pens)} =(x + 3)/(2x + 3) * (x + 2)/(2x + 2)`
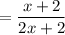
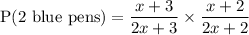
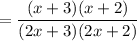`=\frac{(x + 3)(x+2)}{(2x + 3)({2x + 2})}` [2]

The probability of either 2 green pens or 2 blue pens is the sum of the two probability expressions [1] and [2]

`= (x(x -1))/((2x +3)(2x+2)) + \frac{(x + 3)(x+2)}{(2x + 3)({2x + 2})}`

`= (x(x - 1)+ (x + 3) (x +2))/((2x + 3)(2x + 2))\\\\\\= (2x^2+4x+6)/((2x + 3)(2x + 2))\\\\\\\\`

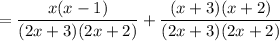
Numerator: factor out 2 to get 2(x² + 2x + 3)

denominator = 4x²+10x+6 = 2 (2x² + 5x + 3)

2 of numerator and 2 of denominator cancel out to give the final expression:

`(x^2\:+\:2x\:+\:3)/(2x^2+\:5x\:+\:3)`

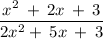
But we are given that the probability of picking 2 pens of the same color = 27/55

This will give us:

`(x^2\:+\:2x\:+\:3)/(2x^2+\:5x\:+\:3) = (27)/(55)`

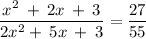
Cross-multiplying we get


`55\left(x^2+\:2x\:+\:3\right)=27\left(2x^2+\:5x\:+\:3\right)`

=>
`55x^2+110x+165 = 54x^2+135x+81`

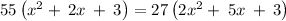
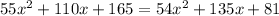
Grouping like terms and simplifying gives

`x^2-25x+84=0`

This is a quadratic equation which can be solved using a scientific calculator (as I did)

The solution set is

x = 21, x = 4

Remember x = number of green pens. We can ignore x = 4 because the total number of pens given by the expression 2x + 3 will be less than 12 and we are told there are more than 12 pens total

So the solution is x = 21 (number of green pens)
Number of blue pens = x + 3 = 21 + 3 = 24

Answer: Green Pens : 21 and Blue Pens: 24