Question

Evaluate this expression

5 - | c+ 1 |

Answer 1

`\quad \huge \quad \quad \boxed{ \tt \:Answer }`

`\qquad \tt \rightarrow \:4\pm c`

____________________________________

`\large \tt Solution \: :`

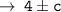
The given expression is :

`\qquad \tt \rightarrow \: 5 - |c + 1|`

`\qquad \tt \rightarrow \: 5 - 1 - |c|`

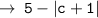
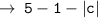
[ as 1 is a positive number, it can come out of modulus function as it is ]

`\qquad \tt \rightarrow \:4- |c|`

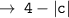
Now, there are two cases possible.

Case 1 :

`\qquad \tt \rightarrow \: 4- c`

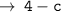
[ if c is a positive number, it will come out of modulus as it is ]

Case 2 :

`\qquad \tt \rightarrow \: 4 - (-c)`

`\qquad \tt \rightarrow \: 4 + c`

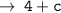
[ if b is a negative number, it will come out of modulus with a negative sign, to make the overall term out of modulus positive ]

Answered by : ❝ AǫᴜᴀWɪᴢ ❞