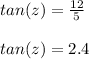Answer:
2.4
Explanation:
tan(theta) is defined as:
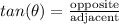
in the given diagram we only have the opposite and hypotenuse, but we can use the Pythagorean Theorem to solve for the other two missing sides.
Pythagorean Theorem:
 , where c is the hypotenuse.
, where c is the hypotenuse.
Plugging in known values we get the following:
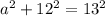
in this case the missing side, or the adjacent side is simply "a"
from here we simplify the bases with exponents

now subtract 144 from both sides
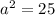
take the square root of both sides

So now we know the adjacent side so we can plug it into the tan equation