
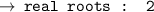
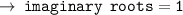
____________________________________
The given polynomial is a 3rd degree polynomial so it has a total of three roots.
And we know, where the curve (of polynomial) cuts the x - axis is its real root. so, from the graph we can infer that the given polynomial has 2 real roots [ as it cuts the x - axis at two points, i.e x = -2 and x = 1 ]
Hence, Number of real roots = 2
Number of imaginary roots = total roots - real roots
i.e 3 - 2 = 1
So, number of imaginary roots = 1
Answered by : ❝ AǫᴜᴀWɪᴢ ❞