Question

TRUE OR FALSE? For any real number x > 0 log 3 x > log ₂ x.​

Answer 1

Answer: False

======================================================

Step-by-step explanation:

We can use a counter-example.

Pick any positive real number you want to replace x.

I'll pick x = 7

Use the change of base formula to get the following

`\log_(3)(\text{x}) = \frac{\log(\text{x})}{\log(3)}\\\\\log_(3)(7) = (\log(7))/(\log(3))\\\\\log_(3)(7) \approx (0.8451)/(0.4771)\\\\\log_(3)(7) \approx 1.7713\\\\`

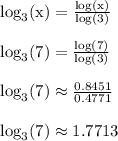
and

`\log_(2)(\text{x}) = \frac{\log(\text{x})}{\log(2)}\\\\\log_(2)(7) = (\log(7))/(\log(2))\\\\\log_(2)(7) \approx (0.8451)/(0.3010)\\\\\log_(2)(7) \approx 2.8076\\\\`

---------------------------

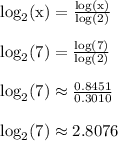
So if x = 7, then we have,

`\log_(3)(\text{x}) > \log_(2)(\text{x})\\\\\log_(3)(7) > \log_(2)(7)\\\\1.7713 > 2.8076\\\\`

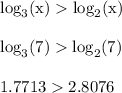
The last statement is false, so the first statement is false when x = 7.

It turns out that you could pick any positive real number for x and will always get a false statement when saying
`\log_(3)(\text{x}) > \log_(2)(\text{x})`