Question

Mr. Burke wants to invest part of his lottery winnings in a safe fund that earns 2.5% annual interest and the rest in a

risky fund that expects to yield 8% annual interest. The amount of money invested in the safe fund, x, is to be exactly
four times the amount invested in the risky fund, y. Use the system of equations to determine the amount to be
invested in each fund if a total of $1080 is to be earned at the end of one year.

Answer 1

eywgw6 the car is in the car is in the car is in

Explanation:

Wu and I will be in the car is in the car is in the car is in the car is here and we can 4

Answer 2

Safe fund = $24,000

Risky fund = $6,000

Explanation:

Definition of variables:

• Let x = the amount of money invested in the safe fund.
• Let y = the amount of money invested in the risky fund.

Given information:

• Safe fund = 2.5% annual interest.
• Risky fund = 8% annual interest.
• Total interest earned at the end of one year = $1080.
• The amount of money invested in the safe fund, x, is to be exactly four times the amount invested in the risky fund, y.

Convert the percentages into decimal form:

`\implies 2.5\%=(2.5)/(100)=0.025`

`\implies 8\%=(8)/(100)=0.08`

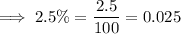
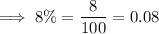
Create a system of equations from the given information and defined variables:

`\begin{cases}0.025x+0.08y=1080\\x=4y\end{cases}`

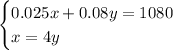
Substitute the second equation into the first equation and solve for y:

`\implies 0.025(4y)+0.08y=1080`

`\implies 0.1y+0.08y=1080`

`\implies 0.18y=1080`

`\implies (0.18y)/(0.18)=(1080)/(0.18)`

`\implies y=6000`

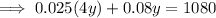
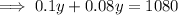
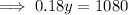
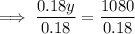
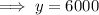
Substitute the found value of y into the second equation and solve for x:

`\implies x=4(6000)`

`\implies x=24000`

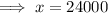
Therefore, the amount invested in each fund was:

• Safe fund = $24,000
• Risky fund = $6,000