Question

I desperately need help. I have been stuck on these 2 questions for maybe 1 day or so. I need an explanation or some sort of understanding because I don't know how to solve these equations.

Can anyone please help me?

Answer 1

first off, let's notice a couple of points on g(x), hmmm say (0 , 5) and (5 , 0) pretty much just the "x" and "y" intercepts, well, to get its equation all we need is two points on it, so let's use those two

`(\stackrel{x_1}{0}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{5}~,~\stackrel{y_2}{0}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{0}-\stackrel{y1}{5}}}{\underset{run} {\underset{x_2}{5}-\underset{x_1}{0}}} \implies \cfrac{ -5 }{ 5 }\implies -1`

`\begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{5}=\stackrel{m}{-1}(x-\stackrel{x_1}{0})\implies {\Large \begin{array}{llll} \stackrel{y}{g(x)}=-x+5 \end{array}}`

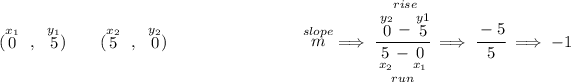
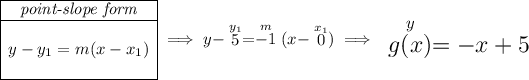
now, let's find f(rx) keeping in mind that f(rx) is really g(x) in disguise

`f(x)=-3x+5\hspace{5em}f(rx)=-3(rx)+5~~ = ~~g(x) \\\\[-0.35em] ~\dotfill\\\\ -3(rx)+5~~ = ~~-x+5\implies -3rx=-x\implies r=\cfrac{-x}{-3x}\implies \boxed{r=\cfrac{1}{3}}`

now as far as the other one goes hmmm well, is simply asking on what "k" is if the y-intercept is -10, however, the equation is already in slope-intercept form, so

`y=-\cfrac{1}{3}x+\cfrac{5}{6}k\qquad \impliedby \qquad \begin{array}c \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array} \\\\[-0.35em] ~\dotfill\\\\ \cfrac{5}{6}k~~ = ~~-10\implies 5k=-60\implies k=\cfrac{-60}{5}\implies \boxed{k=-12}`