Question

Let f(x) =
`2x^2-2x-1`. At which points does the graph of the f(x) have a horizontal tangent line?

Answer 1

The graph has the horizontal tangent line at the the turning point(stationary point) And we know that at the turning point the gradient is 0. We can find the gradient of f(x0 by the first derivative. As I said the gradient a the turning point is 0 meaning since f'(x) =m and m=0 ∴f'(x)=0

`f'(x)=4x-2\\0=4x-2\\4x=2\\(4x)/(4)=(2)/(4) \\x=(1)/(2)`

Now we know that in order to find the point where x =
`(1)/(2)` we can substitute the value of x in the original equation

`f((1)/(2))=2((1)/(2) )^(2) -2((1)/(2) )-1\\f((1)/(2) )=-(3)/(2)`

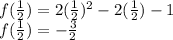
The answer is
`((1)/(2) ,-(3)/(2) )`

Hope I helped.