Question

Give four example of factoring polynomials with Solution​

Answer 1

Explanation:

1) 6x⁷ + 3x⁴ - 9x³

The first step is to identify the greatest common factor. In this case it looks like we can factor a 3 and an x³ out of each term and so the greatest common factor is 3x³

Okay, now let’s do the factoring.

`\sf \small6{x}^(7) + 3{x}^(4) -9{x}^(3)=3{x}^(3) (2{x}^(4) + x - 3)`

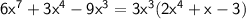
Don’t forget to also identify any numbers in the greatest common factor as well. That can often greatly simplify the problem for later work

2) Factor x^2 - x - 6x

We have

x^2 - x - 6 = (x-3)(x+2).

Note that x^2 - x - 6x can also be expressed as 1 • (x^2 -x - 6)1⋅. Thus, the factors of x^2 - x - 6x are 1, x^2 - x - 6x, x−3 and x+2.

3) Now we have 8ab+8b+28a+28 = 4(2ab+2b+7a+7)

= 4 (2b(a + 1) + 7(a + 1))

= 4(2b + 7)(a + 1)

Thus the factoring polynomials is done by grouping. 8ab + 8b + 28a + 28 = 4(2b + 7)(a + 1)

4) x² + 7x + 12

= x.x + 3x + 4x + 3.4

= x(x + 3) + 4(x + 3)

x² + 7x + 12 = (x + 3)(x + 4)