Question

Add the polynomial. Answer must be in standard form (5x³-6x²+11x-1)+(2x³+3x²-9x+3)

pls pls rlly need help with this​

Answer 1

Answer:
`\boldsymbol{7\text{x}^3-3\text{x}^2+2\text{x}+2}`

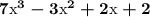
An alternative way to type that is to say 7x^3-3x^2+2x+2

Or you could write 7x³-3x²+2x+2

====================================================

Work Shown:

`(5\text{x}^3-6\text{x}^2+11\text{x}-1)+(2\text{x}^3+3\text{x}^2-9\text{x}+3)\\\\(5\text{x}^3+2\text{x}^3)+(-6\text{x}^2+3\text{x}^2)+(11\text{x}-9\text{x})+(-1+3)\\\\7\text{x}^3-3\text{x}^2+2\text{x}+2\\\\`

----------------

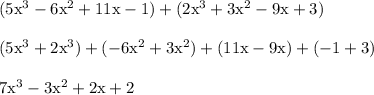
Step-by-step explanation:

In the second step, I grouped like terms. All the cubic terms go in one group, then the squared terms in another, and so on. Afterward, I combined like terms. Add or subtract the coefficients to the left of each variable to do this.

To help see why something like 5x^3+2x^3 = 7x^3, think of it like 5b+2b = 7b where b = x^3. Each b represents a box. 5b means 5 boxes, 2b means 2 boxes. Combining them gets us 5+2 = 7 boxes in total, aka 7b = 7x^3. So this is why we can combine like terms.

But we cannot combine unlike terms such as 5x^3 and 11x since we're talking about different boxes, or different things, at this point. It's like adding apples to oranges.