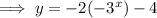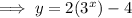Question

Find the exponential equation for the graph.
y =

Answer 1

`y=2(3^x)-4`

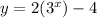
Explanation:

Exponential Function

`\large{\boxed{y=ab^x+c}}`

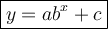
where:

• a is the y-intercept.
• b is the base (growth/decay factor) in decimal form.
• c is the horizontal asymptote.
• x is the independent variable.
• y is the dependent variable.

From inspection of the graph:

• y-intercept = -2
  ⇒ a = -2
• horizontal asymptote: y = -4
  ⇒ c = -4

Substitute the found values of a and c into the formula:

`\implies y=-2(b)^x-4`

To find the value of b, substitute the point on the curve (1, 2) into the formula and solve for b:

`\begin{aligned}y & =-2b^x-4\\\implies 2 & =-2b^1-4\\2 & =-2b-4\\2+4 & =-2b-4+4\\6 & =-2b\\b & =(6)/(-2)\\b & =-3\end{aligned}`

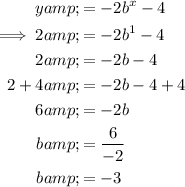
Therefore, the exponential equation of the given graph is:

`\implies y=-2(-3^x)-4`

`\implies y=2(3^x)-4`