Question

Solve x² - 8x + 5 = 0 using the completing-the-square method.

x=4+√11
x=4+√11
x= 4+√5
x=4+√5

Answer 1

Answer:
`\text{x} = 4\pm√(11)`

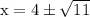
This is the same as writing
`\text{x} = 4+√(11)\ \text{ or } \ \text{x} = 4-√(11)`

========================================================

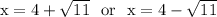
Work Shown:

`\text{x}^2 - 8\text{x} + 5 = 0\\\\\text{x}^2 - 8\text{x} = -5\\\\\text{x}^2 - 8\text{x} + 16 = -5+16\\\\(\text{x}-4)^2 = 11\\\\\text{x}-4 = \pm√(11)\\\\\text{x} = 4\pm√(11)\\\\`

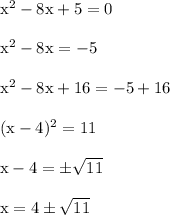
In the third step, I added 16 to both sides so I could complete the square and factor. The 16 is from first dividing the x coefficient -8 in half (to get -4). Then square that result to get (-4)^2 = 16

You can use the quadratic formula to verify each root.