Answer:
77 hours
Explanation:
Sue works:
- Weekdays for $10 an hour.
- Saturdays for $15 an hour.
- Sundays for $20 an hour.
The question suggests that Sue only worked weekdays and Sundays last month as it does not mention Saturday hours.
Assign variables:
- Let x = number of weekday hours Sue worked last month.
- Let y = number of Sunday hours Sue worked last month.
Create two equations with the given information and defined variables:

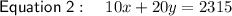
Rewrite the first equation to isolate x:
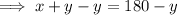

Substitute the found expression for x into the second equation and solve for y:
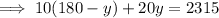
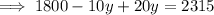
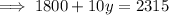
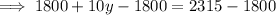
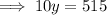
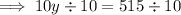
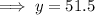
Substitute the found value of y into the first equation and solve for x:
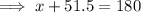
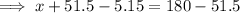
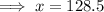
Therefore, Sue worked:
- 128.5 weekday hours
- 51.5 Sunday hours
To find how many more weekday hours than Sunday hours Sue worked last month, simply subtract the found number of Sunday hours from the found number of weekday hours:
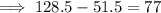
Therefore, Sue worked 77 more weekday hours than Sunday hours last month.