
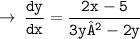
____________________________________
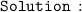
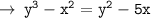
[ take derivative with respect to x, on both sides of the equality ]
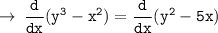
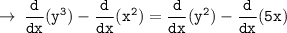
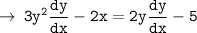
[ By chain rule ]
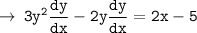
[ take dy/dx common out ]
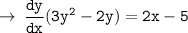
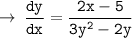
I hope you understood the whole procedure, let me know if you have any problem regarding the steps !
Answered by : ❝ AǫᴜᴀWɪᴢ ❞