Answer:
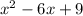
Explanation:
We can check the equations for their answers
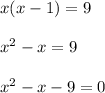
The first equation cannot be factored. If you were to apply the quadratic formula, you would get the two solutions,
 . So this cannot be it
. So this cannot be it
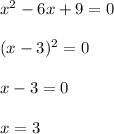
The second equation contains one solution. Let's check the last one.
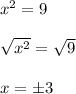
The third equation contains two solutions. Therefore, the second equation is the correct one.