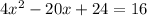Answer:
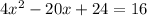
Explanation:
So the bottom without any cuts can be represented as:
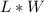 and even after the cuts can be represented in this matter, although L and W will change.
and even after the cuts can be represented in this matter, although L and W will change.
Without the cuts:
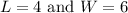
When you cutout the square with side lengths of "x", the length and width decrease by a length of "x", but notice that it's happening twice every side, so it's actually decreasing by 2x.
This means that:
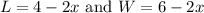
So multiplying these together gives you:
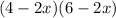
Foiling this out gives you:
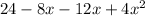
Combining like terms gives you:
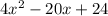
We can solve for "x" by setting this equation equal to 16, since we want the bottom of the box's area to be equal to 16 square inches and this equation represents that.
So the equation to find it would be: