We are here given the coordinates of the vertices of a quadrilateral ABCD which are ,
- A(-6,-1)
- B(-5,2)
- C(0,-2)
- D(-1,-5)
And we need to prove or disprove that it is a llgm . We can do this using the distance formula. We can find the distance between adjacent points and if the measure of opposite sides comes equal then it is a ||gm .
Here opposite sides are AB and CD , and BC and AD .
Distance formula:-
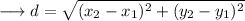
Distance between A and B :-


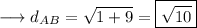
Distance between B and C :-

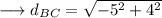
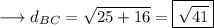
Distance between C and D :-
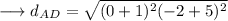
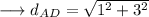
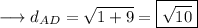
Distance between A and D :-
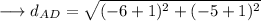
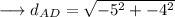
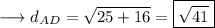
Since the opposite sides are equal, the given coordinates are of a llgm .
And we are done!