Question

Solve the inequality: x+10>2x/5. *

Answer 1

Hello BATAPAAKO!

`\huge \boxed{\mathbb{QUESTION} \downarrow}`

Solve the inequality: x+10>2x/5.

`\large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}`

`x + 10 \gt \frac { 2 x } { 5 } \\`

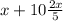
Firstly, multiply both sides of the equation by 5.

`5(x + 10) > 2x \\ = 5x + 50 > 2x`

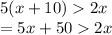
Since 5 is greater than 0, the direction of the inequality will remain unchanged. Now, subtract 2x from both the sides.

`5x + 50 > 20 \\ = 5x + 50 - 2x > 0`

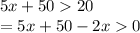
Combine 5x & -2x to get 3x.

`5x + 50 - 2x > 0 \\ = 5x - 2x + 50 > 0 \\ = 3x + 50 > 0`

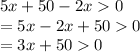
Now, subtract 50 from both the sides. Remember :- anything subtracted by 0 will result in its negation. So 50 subtracted from 0 will give you -50.

`3x + 50 > 0 \\ = 3x > - 50`

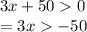
Divide both sides of the equation by 3. Again, since 3 is > 0, the direction of inequality will remain unchanged.

`3x > - 50 \\ = \large\boxed{\boxed{ \bf \: x > - ( 50)/(3) }}`

__________________

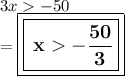
Hope it'll help you!

ℓucαzz ッ