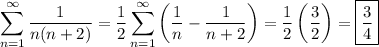Answer:

Explanation:
We have the following series
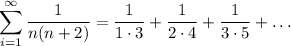
From this series, you can note a telescope series, thus
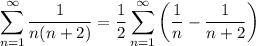
Now we just have to calculate the limit as
For this case we can see that
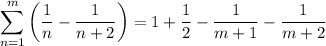
This is because there is a pattern
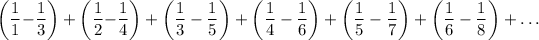
in which every fraction from
 get cancelled, it implies that we are only left with
get cancelled, it implies that we are only left with
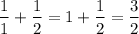
Therefore,