Question

Solve the inequality. z/-2 - 6 < -2

Answer 1

z≥-8

Explanation:
`(z)/(-2)-6 +6 \leq -2 +6\\(z)/(-2) \leq 4\\z \geq -8`

Answer 2

`\textsf{The solution is $\boxed{z \geq -8}$}\:.`

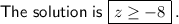
The graph of the solution is attached.

Explanation:

Given inequality:

`(z)/(-2)-6 \leq -2`

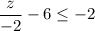
Add 6 to both sides:

`\implies (z)/(-2)-6+6 \leq -2+6`

`\implies (z)/(-2) \leq 4`

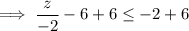
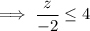
Multiply both sides by -2 (remembering to reverse the inequality sign as we are multiplying by a negative number):

`\implies (z)/(-2) \cdot -2 \leq 4 \cdot -2`

`\implies z \geq -8`

`\textsf{The solution is $\boxed{z \geq -8}$}\:.`

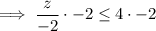
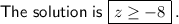
To graph the solution:

• Place a closed circle at -8 as "≥" indicates that -8 is part of the boundary.
• Shade to the right of the closed circle as "≥" means "greater than or equal to".
• Place an arrow (pointing to the right) at the end of the shading to indicate it continues without an end in that direction.