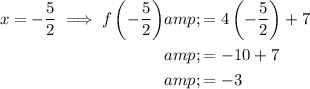Answer:
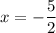
Explanation:
Given:
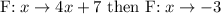
A function, its domain, and its codomain are given as:
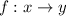
Therefore:
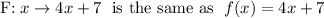
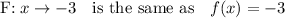
To find the value of x that makes both functions true, equate the functions and solve for x:
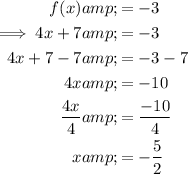
Check by inputting the found value of x into the first function: