Question

a rectangular piece of metal is 5 in longer than its wide. Squares with sides 1 in long or cut from the four corners and the flaps are folded up word to form an open box. if the volume is 546 in^3 ​

Answer 1

Original piece of metal: 23 in × 28 in

Dimensions of the box: 21 in × 26 in × 1 in

Explanation:

Given dimensions of a rectangular piece of metal:

• Width = x in
• Length = (x + 5) in

If squares with sides 1 in long are cut from the four corners, and the flaps are folded upwards to form an open box, 2 inches should be subtracted from the width and the length of the piece of metal. Therefore, the dimensions of the box are:

• Width = (x - 2) in
• Length = (x + 3) in
• Height = 1 in

To find an expression for the volume of the box, multiply the width by the length by the height:

`\begin{aligned}\implies \sf Volume &=\sf width * length * height\\&= (x - 2) * (x + 3) * 1\\& = (x-2)(x+3)\\&=x(x+3)-2(x+3)\\&=x^2+3x-2x-6\\&=x^2+x-6\end{aligned}`

If the volume is 546 in³ then:

`\begin{aligned}\sf Volume&=546\\\implies x^2+x-6&=546\\x^2+x-6-546&=546-546\\x^2+x-552&=0\\x^2+24x-23x-552&=0\\x(x+24)-23(x+24)&=0\\(x-23)(x+24)&=0\\\implies x&=23,-24\end{aligned}`

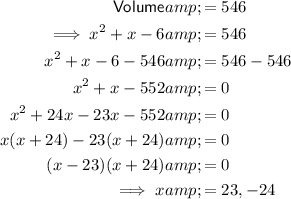
As length is positive, x = 23 only.

To determine the original dimensions of the piece of metal, substitute the found value of x into the expressions for width and length. Therefore, the original dimensions of the piece of metal are:

• Width = 23 in
• Length = 23 + 5 = 28 in

To find the dimensions of the box, substitute the found value of x into the expressions for width and length. Therefore, the dimensions of the box are:

• Width = 23 - 2 = 21 in
• Length = 23 + 3 = 26 in
• Height = 1 in