Question

Use slope to determine if lines PQ and RS are parallel, perpendicular, or neither. Find the slope of line PQ and line RS, then determine the type of lines (parallel, perpendicular, or neither). There should be 3 answers. P(0, -2), Q(0, 7), R(3, -5), S(6, -5)

Answer 1

well, let's check the slope of PQ

`P(\stackrel{x_1}{0}~,~\stackrel{y_1}{-2})\qquad Q(\stackrel{x_2}{0}~,~\stackrel{y_2}{7}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{7}-\stackrel{y1}{(-2)}}}{\underset{run} {\underset{x_2}{0}-\underset{x_1}{0}}} \implies \cfrac{7 +2}{0 }\implies und efined`

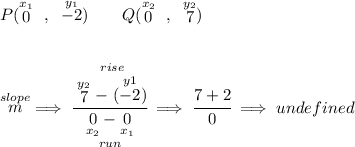
now let's check the slope of RS

`R(\stackrel{x_1}{3}~,~\stackrel{y_1}{-5})\qquad S(\stackrel{x_2}{6}~,~\stackrel{y_2}{-5}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-5}-\stackrel{y1}{(-5)}}}{\underset{run} {\underset{x_2}{6}-\underset{x_1}{3}}} \implies \cfrac{-5 +5}{3}\implies \cfrac{0}{3}\implies 0`

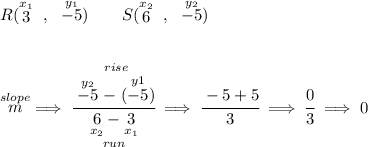
well, oddly enough, only vertical lines have an undefined slope, and only horizontal lines have a slope of 0, meaning that PQ is a vertical line and RS is a horizontal, and well, Check the picture below.