Answer:

Explanation:
Use the slope formula and slope-intercept form.
Slope formula:
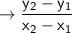
Slope-intercept form:
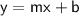
m: slope
b: y-intercept
y₂=(-3.15)
y₁=(-0.25)
x₂=1.8
x₁(-4)
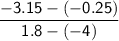
Solve.
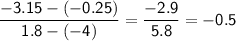
So, the slope is -0.5.
The y-intercept is -2.25.

Therefore, the line passes through the points (-4,–0.25) and (1.8, −3.15) is y=-0.5x-2.25, which is our answer.
I hope this helps, let me know if you have any questions.