Question

Donnesh puts $5,000 into a savings account with a 10% interest rate. How long will it take to double the initial amount?

Answer 1

Answer:We use the formula: A=P(1+r/100)^n where A=future value

Step-by-step explanation:P=present

Answer 2

It will take approximately
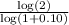`\( (\log(2))/(\log(1 + 0.10)) \)` years for Donnesh to double his initial amount.

To determine the time it takes to double an investment with compound interest, we use the compound interest formula:

`\[ A = P \left(1 + (r)/(n)\right)^(nt) \]`

Where:

- ( A ) is the amount after time ( t ),

- ( P ) is the principal amount (initial investment),

- ( r ) is the annual interest rate (as a decimal),

- ( n ) is the number of times interest is compounded per year, and

- ( t ) is the time in years.

In this case, Donnesh invests $5,000 at a 10% interest rate, meaning ( P = 5000 ) and ( r = 0.10 ). We want to find ( t ) when ( A = 2P ) (double the initial amount), so ( A = 10000 ). Since the interest is compounded annually ( n = 1 ), we can rearrange the formula to solve for ( t ):

`\[ 10000 = 5000 \left(1 + 0.10\right)^t \]`

Solving for ( t ), we get
`\( t \approx (\log(2))/(\log(1 + 0.10)) \).` Utilizing logarithms in the calculation ensures an accurate determination of the time required to double the initial amount.

Understanding compound interest and the associated formula is crucial for making informed financial decisions and assessing investment growth over time.