Answer:
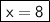
Explanation:
These two bisected angles must be equal for the parallelogram to be a rhombus.
11x-76=7x-44
Isolate the term of x, from one side of the equation.
First you add by 76 from both sides.

Solve.
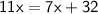
Next, subtract by 7x from both sides.
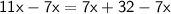
Solve.
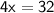
Then, you divide by 4 from both sides.
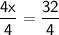
Solve.
Divide these numbers from left to right.
32/4=8
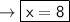
In order for the parallelogram to be a rhombus, x=8.
Therefore, the final answer is x=8.
I hope this helps, let me know if you have any questions.