Answer:
6 meters
Explanation:
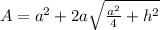 is the formula that you use
is the formula that you use
h=vertical altitude and
a=side length of the base
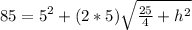
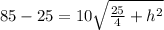
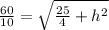
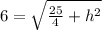

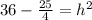
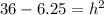
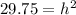
Vertical altitude (h) and
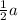 and the slant height form a right triangle with the slant height being the hypotenuse
and the slant height form a right triangle with the slant height being the hypotenuse
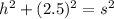 where s=slant height
where s=slant height
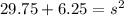

s=6 meters