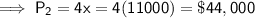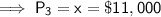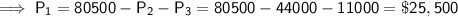Question

What are the 3 equations needed to solve this word problem

Answer 1

First account (4%): P₁ = $25,500

Second account (3¹/₈%): P₂ = $44,000

Third account (2¹/₂%): P₃ = $11,000

Explanation:

Simple Interest Formula

`\large\boxed{\sf I = Prt}`

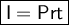
Where:

• I = Total interest accrued.
• P = Principal invested.
• r = Interest rate (in decimal form),
• t = Time (in years),

Given information:

• Total investment = $80,500
• First account: 4% simple interest
• Second account: 3¹/₈% simple interest
• Third account: 2¹/₂% simple interest
• Total interest earned at the end of one year = $2,670

Convert the given percentages into decimal form:

`\implies \sf 4\%=(4)/(100)=0.04`

`\implies \sf 3 (1)/(8)\%=3.125\%=(3.125)/(100)=0.03125`

`\implies \sf 2 (1)/(2)\%=2.5\%=(2.5)/(100)=0.025`

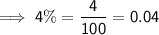
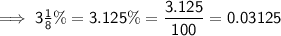
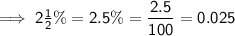
Let P₁, P₂ and P₃ be the principal amounts invested into each of the three accounts, and I₁, I₂ and I₃ be the corresponding interest accrued.

Use the simple interest formula to find expressions for the interest of each account:

`\implies \sf I_1=P_1 \cdot 0.04 \cdot 1=0.04P_1`

`\implies \sf I_2=P_2 \cdot 0.03125 \cdot 1=0.03125P_2`

`\implies \sf I_3=P_3 \cdot 0.025 \cdot 1=0.025P_3`

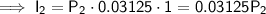
Let x be the amount invested in third account.

Therefore, the amount invested in the second account = 4x.

The total interest earned is $2,670:

`\begin{aligned}\textsf{Total interest}&=\sf 2670\\\implies \sf I_1+I_2+I_3&=\sf 2670\\ \sf 0.04P_1+0.03125P_2+0.025P_3&= \sf2670\\\sf 0.04P_1+0.03125(4x)+0.025(x)&= \sf2670\\\sf 0.04P_1+0.125x+0.025x&= \sf2670\\\sf 0.04P_1+0.15x&= \sf2670\\\end{aligned}`

The total amount invested it $80,500:

`\begin{aligned} \textsf{Total principal} & = \sf 80500\\\implies\sf P_1+P_2+P_3 &=\sf80500\\\sf P_1+4x+x&=\sf 80500\\\sf P_1+5x&=\sf 80500\\\sf P_1&=\sf 80500-5x\end{aligned}`

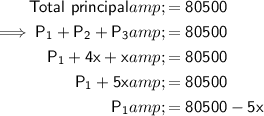
Substitute the expression for P₁ into the total interest equation and solve for x:

`\begin{aligned}\sf 0.04P_1+0.15x & = \sf 2670\\\implies \sf 0.04(80500-5x)+0.15x & = \sf 2670\\\sf 3220-0.2x+0.15x & = \sf 2670\\\sf 3220-0.05x & = \sf 2670\\\sf 550&=\sf0.05x\\\sf x&=\sf 11000\end{aligned}`

Therefore:

`\implies \sf P_2=4x=4(11000)=\$44,000`

`\implies \sf P_3=x=\$11,000`

`\implies \sf P_1=80500-P_2-P_3=80500-44000-11000=\$25,500`