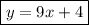Question

Let f be a differentiable function with f(-1) = -5 and f'(-1) = -1. Let the function g(x) = x² f(x). Write the equation of the line tangent to the graph of g at the point where x = -1.

Answer 1

`y=9x+4`

Explanation:

Differentiation is an algebraic process that finds the gradient of a curve.

At a point, the gradient of a curve is the same as the gradient of the tangent line to the curve at that point.

Given function:

`g(x)=x^2 \:f(x)`

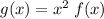
Differentiate the given function using the product rule.

`\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\frac{\text{d}y}{\text{d}x}=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}$\\\end{minipage}}`

Identify u and v and differentiate them with respect to x:

`\text{Let $u=x^2 \implies \frac{\text{d}u}{\text{d}x}=2x$}`

`\text{Let $v=f(x) \implies \frac{\text{d}v}{\text{d}x}=f'(x)$}`

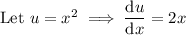
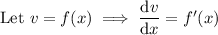
Put everything into the product rule formula:

`\begin{aligned}\implies \frac{\text{d}y}{\text{d}x} & =u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}\\& = x^2 \cdot f'(x)+f(x) \cdot 2x\\& = x^2\:f'(x)+2x\:f(x)\end{aligned}`

Given:

`f(-1)=-5`

`f'(-1)=-1`

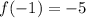
To find the gradient of the curve at x = -1, substitute x = -1 into the differentiated function:

`\begin{aligned}x=-1 \implies \frac{\text{d}y}{\text{d}x} & =(-1)^2\:f'(-1)+2(-1)\:f(-1)\\& =(1)(-1)+(-2)(-5)\\& =-1+10\\& =9\end{aligned}`

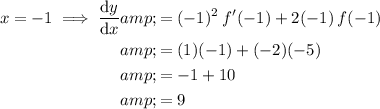
Therefore, the gradient of the curve at x = -1 is 9.

`\begin{aligned}\textsf{When $x = -1$} \implies g(-1)&=(-1)^2 \cdot f(-1)\\& = 1 \cdot (-5)\\& = -5\end{aligned}`

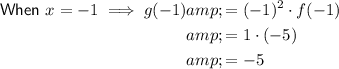
Therefore, the point on the function is (-1, -5).

Substitute the found gradient and the point into the point-slope form of a linear equation:

`\begin{aligned}y-y_1 & =m(x-x_1)\\\implies y-(-5)&=9(x-(-1))\\y+5&=9(x+1)\\y+5&=9x+9\\y&=9x+4\end{aligned}`

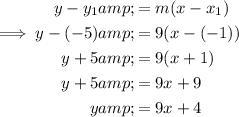
Therefore, the equation of the line tangent to the graph of g at the point where x = -1 is:

`\boxed{y=9x+4}`