Question

What are the solutions to the equation 4x^2 = 28?

Answer 1

x=
`√(7)`,
`- √(7)`

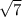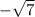
Explanation:

this is your equation

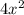`4x^(2)` = 28

first you bring 28 to the other side of the equal sign like this

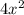`4x^(2)` - 28 = 0

then you find the common factor. the common factor in both numbers is 4 so you pull that number out. it will be like this

4(
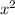`x^(2) \\` - 7) = 0

after that you will divide both sides with the factor (4) to get
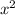`x^(2)` - 7 by itself

`(4(x^(2) - 7) )/(4)` =
`(0)/(4)`

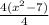once you do that you will get

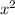`x^(2) \\` - 7 = 0

so your equation is written in this form

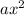`ax^(2)`+bx+c=0

so now look at your equation 1
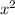`x^(2) \\` - 7 = 0 and fill in the values for a, b and c.

A= 1

B=0, because there is no bx in you equation, you just put a 0

C= -7

now you will use the quadratic formula.

so now in your quadratic formula fill in the values for a, b, and c.

x= -0 +-
`\frac{\sqrt{0^(2) -4*1*-7 } }{2*1}`

we are half way done!

all you have to do is solve.
1) evaluate the exponent

x= 0 +-
`(√(0 -4*1*-7 ) )/(2*1)`

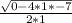
2) multiply the numbers

x= 0 +-
`(√(0+28) )/(2*1)`

3) add the numbers

x= 0 +-
`(√(28) )/(2*1)`

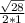
4) evaluate the square root. at the same time you can multiply the denominator

x= 0 +-
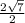`(2√(7) )/(2)` how to evaluate the square root:

`√(4) *√(7)`

`2√(7)`

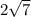
5) add the 0

now after all this you are left with 2 separate equations

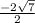`(-2√(7) )/(2)` and
`(2√(7) )/(2)`

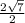
now cut the twos form the numerator and the denominator

finally you are left with your answers!

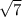`√(7)` and
`-√(7)`

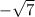
Done!!