Question

NO LINKS!! Please help with questions 5-8​

Answer 1

`{ \qquad\qquad\huge\underline{{\sf Answer}}}`

Here's the translation we need to make :

pre image to image : (x , y) to (x - 8 , y + 4)

Problem : 5

Image of A (2 , 6) : -

`\qquad \sf  \dashrightarrow \: (2 - 8 , 6 + 4)`

`\qquad \sf  \dashrightarrow \: ( - 6 , 10)`

Problem : 6

`\qquad \sf  \dashrightarrow \: ( - 1 - 8 , 5 + 4)`

`\qquad \sf  \dashrightarrow \: ( - 9 , 9)`

image to pre - image : (x - 8 , y + 4) to (x , y)

in other words, it can be expressed as :

image to pre - image : (x , y) to (x + 8 , y - 4)

Problem : 7

`\qquad \sf  \dashrightarrow \: ( - 3 + 8 , - 10 - 4)`

`\qquad \sf  \dashrightarrow \: (5 , - 14)`

Problem : 8

`\qquad \sf  \dashrightarrow \: (4 + 8 , - 3 - 4)`

`\qquad \sf  \dashrightarrow \: (12 , - 7)`

Answer 2

Problem 5

Answer: (-6,10)

---------------

Step-by-step explanation:

We subtract 8 from the x coordinate and add 4 to the y coordinate. This shifts the point 8 units left and 4 units up.

`(\text{x},\text{y})\to(\text{x}-8,\text{y}+4)\\\\(2,6)\to(2-8,6+4)\\\\(2,6)\to(-6,10)\\\\`

This shifts the point A(2,6) to A'(-6,10)

========================================================

Problem 6

Answer: (-9, 9)

---------------

Step-by-step explanation:

Follow similar steps as the previous question.

`(\text{x},\text{y})\to(\text{x}-8,\text{y}+4)\\\\(-1,5)\to(-1-8,5+4)\\\\(-1,5)\to(-9,9)\\\\`

========================================================

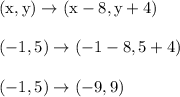
Problem 7

Answer: (5, -14)

---------------

Step-by-step explanation:

The previous two problems gave us a preimage and asked to find the image. This time we're given an image point and want to find the preimage. We go in reverse.

What we'll need to do is find the inverse transformation.

• The opposite of "shift 8 units left" is "shift 8 units right".
• The opposite of "shift 4 units up" is "shift 4 units down".

Therefore, the inverse of
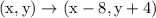`(\text{x},\text{y})\to(\text{x}-8,\text{y}+4)\\\\` is
`(\text{x},\text{y})\to(\text{x}+8,\text{y}-4)\\\\`

Simply flip the signs.

Now that we have the inverse, we can then find the preimage for C'(-3,-10) through basically the same type of steps as the previous two problems. Plug in the coordinates to find that...

`(\text{x},\text{y})\to(\text{x}+8,\text{y}-4)\\\\(-3,-10)\to(-3+8,-10-4)\\\\(-3,-10)\to(5,-14)\\\\`

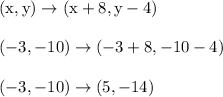
So if C'(-3,-10) is the image point, then its corresponding preimage point is C(5,-14)

To check the answer, let's apply the original transformation to point C and we should get to (-3,-10)

`(\text{x},\text{y})\to(\text{x}-8,\text{y}+4)\\\\(5,-14)\to(5-8,-14+4)\\\\(5,-14)\to(-3,-10)\\\\`

This confirms we have the correct preimage point.

========================================================

Problem 8

Answer: (12, -7)

---------------

Step-by-step explanation:

We follow the same idea as problem 7. Using the inverse transformation on the coordinates of D'(4, -3) gets us this:

`(\text{x},\text{y})\to(\text{x}+8,\text{y}-4)\\\\(4,-3)\to(4+8,-3-4)\\\\(4,-3)\to(12,-7)\\\\`

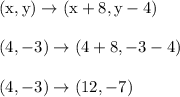
I'll let you check this answer by plugging the coordinates of (12,-7) into the original transformation. You should get (4,-3) as a result.