Answer:
6.2 seconds
Explanation:
Given function: h(t) = – 0.145t² + 0.019t + 5.5
- Here h(t) which determines the height, when Frisbee touches the ground, the height shall be 0.
solve the quadratic equation:
using the formula:
![\left[\begin{array}{ccc} t = ( -b \pm √(b^2 - 4ac))/(2a)\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/college/wwjhwvxgvlk6vichczzsqglb984lly0kac.png)
Solving steps:
→ –0.145t² + 0.019t + 5.5 = 0
→ [–0.145t² + 0.019t + 5.5 = 0 ]* 100
→ -145t² + 19t + 5500 = 0
→
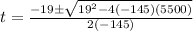
→
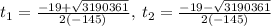
→
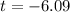 ,
,
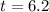
→
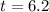
Time cannot be negative here.
- So time taken: 6.2 seconds.