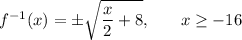Answer:
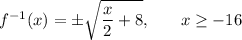
Explanation:
Given function:
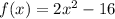
The given function has an unrestricted domain and a restricted range.
- Domain of f(x): (-∞, ∞)
- Range of f(x): [-16, ∞)
Inverse of a function
f⁻¹(x) is the notation for the inverse of the function. The inverse of a function is its reflection in the line y = x.
To find the inverse of the given function, swap f(x) for y:
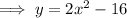
Rearrange the equation to make x the subject:
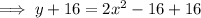
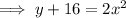


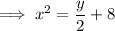
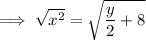

Swap the x for f⁻¹(x) and the y for x:
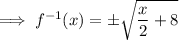
The domain of the inverse function is the range of the function.
Therefore, the domain of the inverse function is restricted:
- Domain of f⁻¹(x): [-16, ∞)
Solution