Question

Factorise n2-mn

the 2 is supposed to mean squared
​

Answer 1

n(n - m)

Explanation:

n² - mn ← factor out n from each term

= n(n - m)

Answer 2

n(n-m)

Explanation:

We are given the quadratic expression:-

`\displaystyle \large{ {n}^(2) - mn}`

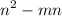
To factor this expression, do you notice that there are two n's in the expression? Yes, since in the expression, the whole terms have n-term; what we are going to do is to common factor n out!

So how do we do that? Simple, just pull n out.

`\displaystyle \large{n( {n} - m)}`

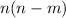
From above, you might be wondering how does it turn out like this. Do not worry, I've got you!

When we pull n out of the expression, we just divide the expression by n.

Don't get it? Let me show you!

Step 1 - Form the expression:

`\displaystyle \large{ {n}^(2) - mn}`

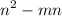
Step 2 - Pull n out and bracket the expression.

`\displaystyle \large{n( {n}^(2) - mn)}`

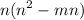
Step 3 - Divide the expression by n.

`\displaystyle \large{n( \frac{ {n}^(2) - mn}{n})} \\ \displaystyle \large{n( n - m)}`

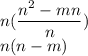
Still not get it? Well, let's demonstrate another method.

Let's say we have the expression again!

`\displaystyle \large{ {n}^(2) - mn}`

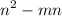
Since n^2 comes from n•n.

`\displaystyle \large{ n \cdot n - mn}`

Bracket the expression:

`\displaystyle \large{ (n \cdot n - mn)}`

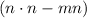
Now let's imagine that these two brackets are the doors.

m-term: There are so many of you in this bracket house! If this keeps continuing, this bracket house might be collapsed!

3 n-terms were shocked! They had to find the ways to protect their bracket house, the legacy that their cases parents gave.

But then the 2 n-terms did an unexpected! They decided to help them by going outside of the bracket house and stand there!

m-term: Why there is only one n-term outside when two of them left?

another n-term: Well, the another n-term finds food for themselves and the another one there guards our bracket house.

The End!

As we get:

`\displaystyle \large{n ( n - m)}`

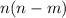
Not clearing all your doubts? Let me know or ask your doubts under my comment!