Question

Find the equation of this line(image)

Answer 1

Answer:
`y = (1)/(2)x + 1`

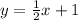
Explanation:

We first want to find the slope of the line. We can do this by using the equation (m represents slope):
`m = (y_(2) - y_(1))/(x_(2) - x_(1))`

We want to pick two coordinates to plug in to this equation. I will use the coordinates chosen in the problem, (0, 1) and (4, 3):

`m = (3 - 1)/(4 - 0) = (2)/(4) = (1)/(2)`

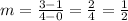
Now that we know the slope, we must identify the y-intercept. We do this by finding what the y-value equals in the function when x = 0. In this case, it is shown that when x = 0, y = 1.

This means that following the equation:
`y = mx + c`

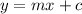
Where c is the y-intercept, we get the answer:
`y = (1)/(2)x + 1`

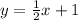
I hope this helps. If you need anything else explained please let me know.