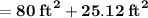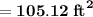Question

Find the area of this figure. Round your answer to the nearest hundredth. Use 3.14 to approximate pi. 8ft by 10ft

Answer 1

`\large \bf \implies{105.12 \: {ft}^(2) }`

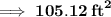
Explanation:

`\bf{Semi \: rectangle \: = \: length \: × \: width }\\ \\ \bf{Semi \: circle \: = \: \pi{r}^(2) } \: \: \: \: \: \: \: \bigg [r = (d)/(2) \bigg ] \\ \\ \bf{ S \: = \: 8 * 10 + (1)/(2) * \pi * \bigg( (8)/(2) \bigg)^(2) } \\ \\ \bf{= 80 + (1)/(2) * 3.14 * {4}^(2) }\: \: \: \: \: \: \\ \\ \bf{= 105.12 \: {ft}^(2) } \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \:`

`\: \: \:\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \bf{OR}`

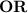
We can divide the area in two parts :

1. The left part is a rectangle with length 10ft and width 8ft
2. The right part is a semicircle with diameter 8ft.

So, Area of the left rectangular part

= length x width

= 10 × 8 ft²

= 80 ft²

Now, diameter of the semicircular part = 8 ft

So, radius

=
`\bf(diameter)/(2)`

=
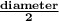
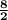`\bf(8)/(2)` ft

= 4 ft

So, area of the right semicircular part

`\bf{= (1)/(2) * \pi * radius^2}`

`\bf{= (1)/(2) * 3.14 × 4^2 ft^2}`

`\bf{= 25.12 \: ft^2}`

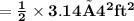
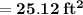
Total area ,

= Area of the left rectangular part + Area of the right semicircular part

`\bf{= 80 \: {ft}^(2) + 25.12 \: {ft}^(2)}`

`\bf{= 105.12 \: {ft}^(2) }`