Answer:
c ≈ 16.55cm ; ∠A = 65 degrees ; ∠B = 25 degrees
Explanation:
Because of the Pythagorean theorem, we can solve for c.
This theorem states: a^2 + b^2 = c^2
Since there can only be 180 degrees in a triangle, angle C must be our largest angle. This means that side c is our hypotenuse (the longest side).
Using all of this information, we can say that 15^2 + 7^2 = c^2.
Simplifying that equation, we get that 274 = c^2.
In order to find c, we must square root both sides, and we find that c is about 16.55 cm long.
Using SOHCAHTOA, we know that the tan(∠B)=
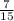 . Therefore, the arctan (
. Therefore, the arctan (
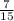 ) = ∠B.
) = ∠B.
Once you find that ∠B is about 25 degrees, you can add ∠B and ∠C together and subtract that from 180 to find ∠A.
∠A = 65 degrees.