Answer:
See attachment for graph.
Explanation:
When graphing inequalities:
- < or > : dashed lines.
- ≤ or ≥ : solid line.
- < or ≤ : shade under the line.
- > or ≥ : shade above the line.
Given inequality:
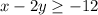
Rearrange the equation to isolate y:
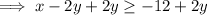
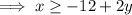
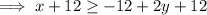
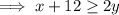
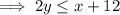
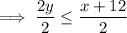
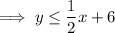
Find two points on the line by substituting two values of x into "y=":
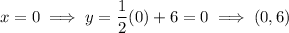
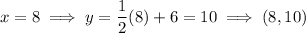
Plot the points and draw a straight solid line through them.
As the inequality is "y ≤", shade below the line.