Answer:

x is between 7 and 10; including 7 but excluding 10
========================================================
Step-by-step explanation:
Let's isolate x. First add 4 to all sides. Then divide all sides by 2.
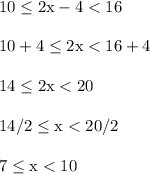
The solution set is anything between 7 and 10. We include 7, but exclude 10.
The graph has a closed filled in circle at 7 and an open hole at 10. Shade in between those endpoints to fully describe the solution set.