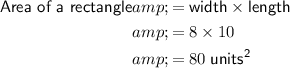Answer:
80 units²
Explanation:
Given vertices of a rectangle:
- A = (-8, 5)
- B = (2, 5)
- C = (2, -3)
- D = (-8, -3)
As points A and D share the same x-coordinate, and points B and C share the same x-coordinate, the difference between the different x-coordinates is the length of the rectangle:
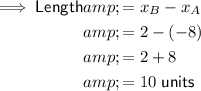
As points A and B share the same y-coordinate, and points C and D share the same y-coordinate, the difference between the different y-coordinates is the width of the rectangle:
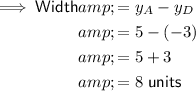
Therefore: