The equation of the line is
![\[x -2= -(1)/(5)(y - 1)^2 \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/1o1mobrt4u39k09vst8l5m2xi42n8o6ksk.png) , the vertex is
, the vertex is
 , the focus is
, the focus is
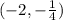 , and the directrix is
, and the directrix is
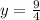 .
.
To rewrite the given equation
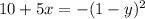 in the form
in the form
 , let's complete the square:
, let's complete the square:
![\[10 + 5x = -(1 - y)^2\]](https://img.qammunity.org/2023/formulas/mathematics/high-school/xf963j8cy45xxjfiwbgko0dbmtcvp3tijh.png)
First, move the constant term (10) to the other side:
![\[5x = -(1 - y)^2 - 10\]](https://img.qammunity.org/2023/formulas/mathematics/high-school/hajfn5d8mdj5x9axviu51w5ovelt0y5tqv.png)
Divide both sides by 5:
![\[x = -(1)/(5)(1 - y)^2 - 2\]](https://img.qammunity.org/2023/formulas/mathematics/high-school/k3m7y1so3k3azu403ztzyszpwjf0qt1qu6.png)
Now, rewrite it in the form
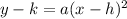 :
:
![\[x = -(1)/(5)(1 - y)^2 - 2\]](https://img.qammunity.org/2023/formulas/mathematics/high-school/k3m7y1so3k3azu403ztzyszpwjf0qt1qu6.png)
![\[x = -(1)/(5)(y - 1)^2 - 2\]](https://img.qammunity.org/2023/formulas/mathematics/high-school/u1feenswtg6xk3n243ehh5dhgybhh9sjf4.png)
Now, the equation is in the form
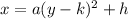 , where
, where
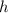 is the x-coordinate of the vertex and
is the x-coordinate of the vertex and
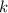 is the y-coordinate of the vertex.
is the y-coordinate of the vertex.
Comparing with the general form
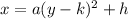 , we have
, we have
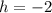 and
and
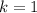 .
.
So, the vertex is
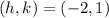 .
.
Now, let's find the focus and directrix.
The general form of a vertical parabola is
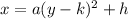 , and its focus is given by
, and its focus is given by
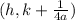 , while the directrix is a horizontal line given by
, while the directrix is a horizontal line given by
 .
.
In our case,
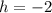 and
and
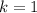 , so the focus is at
, so the focus is at
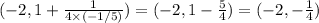 .
.
The directrix is the horizontal line
 .
.
So, the vertex is
 , the focus is
, the focus is
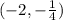 , and the directrix is
, and the directrix is
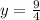 .
.