Answer:
d. x=4
Explanation:
So we have the following equation:
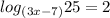
Now to understand how we can rewrite this equation, let's go over the definition of a log:
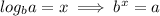
So this value of "log base b of a" Is equal to the value that I have to raise the base b to, to get the result a
So when I have the equation:
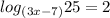
This is essentially saying, I have to raise (3x-7) the base, to the power of 2, to get the result of 25
So let's rewrite it using the definition of a log
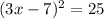
Take the square root of both sides
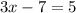
add 7 to both sides
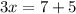
Now divide both sides by 3
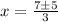
Simplifying:
