Answer:
5.93 m/s (2 d.p.)
Step-by-step explanation:
When a body is projected through the air with initial speed u, at an angle of θ to the horizontal, it will move along a curved path.
Therefore, trigonometry can be used to resolve the body's initial velocity into its vertical and horizontal components:
As the projectile is modeled as moving only under the influence of gravity, the only acceleration the projectile will experience will be acceleration due to gravity.
Constant Acceleration Equations (SUVAT)

When using SUVAT, assume the object is modeled as a particle and that acceleration is constant.
If the salmon jumps at an angle of 36.2° then:
Resolving horizontally
The horizontal component of velocity is constant, as there is no acceleration horizontally.
Resolving horizontally, taking → as positive:
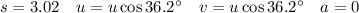
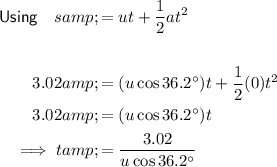
Resolving vertically
Acceleration due to gravity = 9.81 ms⁻²
Resolving vertically, taking ↑ as positive and using the found expression for t:
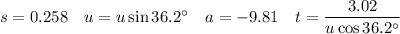

Therefore, the minimum speed at which the salmon should leave the water is 5.93 m/s (2 d.p.).